О расчете круглых колонн (продолжение)

 Как посчитать рамный узел ? 

В предущей статье, посвященной расчету круглых колонн, мы разобрали ряд вопросов по проверке общей несущей способности стержня.

Но надежность конструкции часто определяется не расчетом самого элемента, а его локальных мест нагружения в узлах.

https://t.me/steelintouch

Сегодня рассмотрим расчет колонны в жестком узле. 

В узле примыкают разнонагруженные ригели одинаковой высоты (104 см). Накладки в уровне верхней и нижней полки прорезные, общие, примыкание ригелей под 90 градусов относительно друг друга. 

Колонна сечением 720х10, верхний конец свободен, нижний закреплен по всем направлениям.

Рис.1 Основные габаритные размеры узла и прикладываемые нагрузки

Несмотря на все кажущееся обилие справочной литературы по рамным конструкциям, указания по узлам трубчатых конструкций практически не встречаются.

Если проверку примыкающих частей ригеля можно произвести по общепринятым  правилам для рамных узлов, то как проверять круглую колонну в рамном узле не совсем понятно. Нужно искать аналогии.

В общем случае проверка стенки колонны должна быть выполнена по формуле из [1]:

 (1)

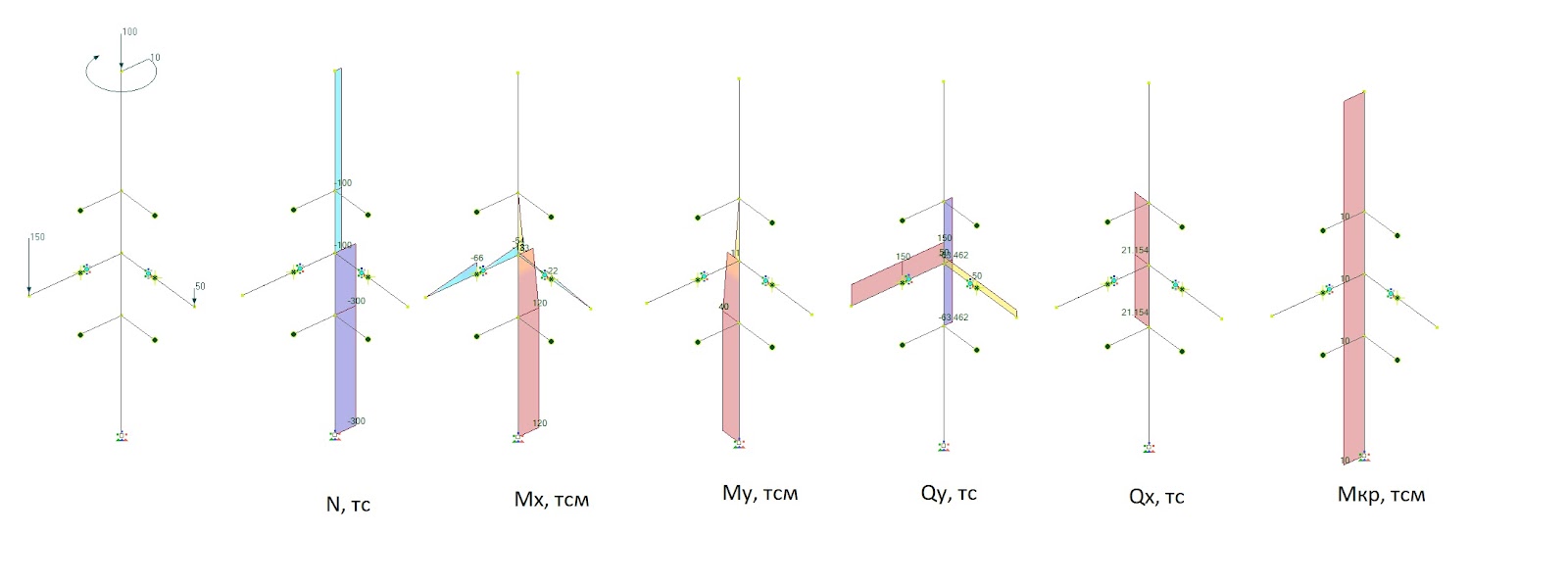
Эпюры усилий в стержне колонны в пределах рамного узла выглядят так (как их получить в корректном виде см. тут):

Рис.2 Расчетная схема узла, эпюры усилий

При этом Mкр - это момент чистого кручения, который обсуждался тут.

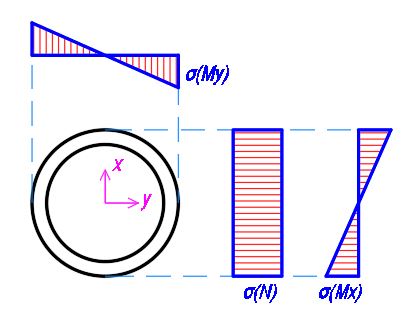
Эпюры напряжений в кольцевом сечении от вышеприведенных усилий выглядят так:

Рис.3 Эпюры нормальных напряжений

Рис.4 Эпюры касательных напряжений

Ближайшая аналогия, подходящая по смыслу - это промышленные трубопроводы больших диаметров. Согласно [2] суммарные величины нормальных и касательных напряжений для подстановки в ф-лу (1) можно определить по формулам для оболочки кольцевого сечения:

(2)

Здесь угол "бэта" характеризует  координату точки сечения, для которой определяются напряжения (см. рис.8).

Это означает, что задача сводится к поиску такой точки на поверхности трубы при произвольном угле "бэта", где в сложном напряженном состоянии приведенные напряжения [ф-ла (1)] будут максимальными.

Причем при одновременном действии поперечных сил в двух направлениях, в той точке, где касательные напряжения от действия силы одного направления максимальные, от силы другого направления они равны нулю (см. рис.4).

Поэтому в формулах (2) в расчете результирующего "тау" стоит знак минус. 

Для расчетной ситуации по рис.2 максимальное значение приведенных напряжений  по ф-ле (1), (2) достигается при угле "бэта" примерно равном 17 градусов и составляет 3842 кг/см2.

Рассмотрим работу узла в МКЭ-модели с нагрузками  согласно рис.2.

 

Рис.5 Общий вид расчетной схемы

Первое, что нужно отметить - резкую концентрацию приведенных напряжений в колонне под более нагруженным примыкающем ригелем. Это объясняется тем, что в данной зоне поперечная сила примыкающего ригеля уже полностью передана на колонну, при этом момент под ригелем максимальный (см. рис.2). Это обстоятельство может быть принципиальным для тонкостенных труб, когда скалывающие напряжения в зоне под ригелем будут велики.

Рис.6 Приведенные напряжения в стенке колонны под опорой ригеля

Максимальные приведенные напряжения в колонне в зоне узла возникают вблизи нижней полки более загруженного ригеля в точке под углом "бэта" 16 градусов со значением 3824 кг/см2, что согласуется с ручным расчетом.

Рис.7 Приведенные напряжения в стенке в зоне узла

Рис.8 Угол "бэта", соответствующий точке с максимальными приведенными напряжениями

Отдельно нужно рассмотреть учет продольной силы в колонне в зоне узла. Ее величина складывается из усилия в колонне выше узла и поперечной силы в примыкающих ригелях. В стержневой расчетной схеме (см. рис.2) условно принято, что поперечная сила от примыкающих ригелей передана в уровне оси ригеля, поэтому продольная сила на эпюре N в уровне нижних поясов имеет полное значение 300 тс. При учете в ф-ле (2) данного значения N нормальные напряжения увеличатся существенно (на 900 кг/см2 или 25%). 

Но в МКЭ-модели этого не происходит (рис.9).

Рис.9 Нормальные напряжения в зоне узла от моментов в примыкающих ригелях (слева) и от моментов+поперечных сил (справа)

При сравнительном расчете модели с передачей момента с ригеля без поперечной силы и с поперечной силой в отсутствие других силовых факторов увеличение максимальных нормальных напряжений составило 5%. 

Это можно объяснить тем, что стенка ригеля приварена к полке колонны по всей своей высоте и передает опорную Q на всей его длине (а не в условной точке как принято на рис.2). Усилие оказывается полностью переданным только в уровне нижней полки ригеля и не успевает в пределах узла распределится на все сечение колонны. Поэтому происходит концентрация напряжений в области под этой полкой(рис.8). Вдобавок в состав поперечного сечения колонны в зоне узла входят приопорные участки стенок ригеля, которые частично включаются в работу, влияя на распределение напряжений в узле. 

Поэтому можно предположить, что принимать в расчет полное значение продольной силы некорректно, поскольку при больших поперечных силах получится сильно завышенное значение приведенных напряжений.  

Вопрос в каком размере брать данную силу в расчет требует уточнения по типу того, как это предлагается выполнять в статье [4] для двутавровых колонн. 

Если вы знаете как это можно сделать или вам известны другие способы и расчетные методики таких узлов, пишите в комментариях.

[1] СП 16.13330.2017 "Стальные конструкции с изменениями №1...4"

[2] "Проектирование промышленных трубопроводов" М.И. Казакевич, Киев 1989

[3] "Справочное пособие по сопротивлению материалов. Издание третье" М.Н. Рудицын, Минск 1970

[4] "Исследование действительной работы сварного рамного узла и рекомендации по его расчету" П.Н. Троицкий, Москва 1977